第 1 章 定解问题
封面图片 PID:1628397182442
数学物理方程相关内容 导航栏
本系列可能涉及到的前置课程(顺序不代表重要程度):
- 大学物理
- 数学分析/高等数学
- 高等代数/线性代数
- 实变函数与泛函分析
- 常微分方程
- 复变函数
- 解析几何
其中常微分方程是本系列的核心基础课程。
引言
引言
数学物理方程的研究对象是自然科学和工程技术各门分支中出现的一些偏微分方程,它涉及自然科学和工程技术的各个领域。数学物理方程注重于使用一些非数值方法来求解这些方程,比起纯数学理论更注重计算过程,是一门偏工科的课程。本系列就以吴小庆教授编著的《数学物理方程》[^1]为基础,结合我的课堂笔记和其他相关资料,简述这一门课程的内容。系列的组织结构大体如下:
第 1 章:定解问题。本章以《数学物理方程》第 1 章内容为基础,介绍定解问题和相关理论,包括偏微分方程的基本概念,三类典型偏微分方程的建立和二阶线性偏微分方程的分类等。
第 2 章:分离变量法。本章以《数学物理方程》第 2、7 章内容为基础,介绍分离变量法的基本概念,以及分离变量法的应用,包括平面直角坐标系、极坐标系、柱坐标系和球坐标系下的分离变量法。
第 3 章:积分变换法。本章以《数学物理方程》第 6、8 章内容为基础,介绍积分变换法的基本概念,以及积分变换法的应用,包括拉普拉斯变换和傅里叶变换和格林函数法等。
第 4 章:偏微分方程的级数解法。本章以《数学物理方程》第 3-5 章内容为基础,介绍级数解法的基本概念,以及级数解法的应用,包括广义傅里叶变换、施图姆-刘维尔(Strutm-Liouville)问题、贝塞尔方程、勒让德多项式等。
第 5 章:算子级数法。本章以《数学物理方程》第 9 章内容为基础,介绍算子级数法的基本概念,以及算子级数法的应用等。
第 1 章 定解问题
第 1 章 定解问题
偏微分方程正问题(即定解问题),是研究由偏微分方程描述某种物理过程或现象,并根据系统的状态变量的某些特定条件(包括初始条件,边界条件等)来确定整个系统的状态变量的变化规律,即研究状态的数学表达式
1.1 偏微分方程的一般概念
1.1 偏微分方程的一般概念
1.1.1 基本概念
偏微分方程是含有未知多元函数及其偏导数的关系式。
例如,$$a(x, y)u_x + b(x, y)u_y + c(x, y)u = 0, \tag{1.1.1}$$
其中 $a,b,c$ 为已知函数, $u = u(x, y)$ 为未知函数。
$$\frac{\partial u}{\partial t} = a^2\frac{\partial^2 u}{\partial x^2}, \tag{1.1.2}$$
$$uu_{xy} + u_x = u, \tag{1.1.3}$$
都是偏微分方程。
一个偏微分方程所含有的未知函数的最高阶导数的阶数称为偏微分方程的阶。如方程 (1.1.1) 是一阶偏微分方程, 方程 (1.1.2), (1.1.3) 是二阶偏微分方程。
若偏微分方程中各项关于未知函数及其偏导数都是一次的,则称这个方程为线性方程,否则为非线性方程。如方程 (1.1.1) 是线性方程,方程 (1.1.2), (1.1.3) 是非线性方程。若非线性方程中,关于未知函数的所有最高阶偏导数都是线性的,则其为拟线性方程,如方程 (1.1.3) 是拟线性方程。
线性方程中,称方程中不含有未知函数及其偏导数的项为自由项,若方程的自由项恒为零,称方程是齐次方程,否则为非齐次方程。例如,方程 (1.1.1) 是齐次方程,方程 (1.1.2) 是非齐次方程。
若某函数在指定区域内连续,具有方程中出现的一切偏导数,且将其代入方程使方程成为恒等式,则称此函数为该区域内方程的解。
1.1.2 线性算子
限于篇幅,本节仅讨论偏微分方程理论中的微分线性算子。
算子是一种数学法则,把它作用到一个函数上时,便产生另一个函数。例如表达式 $$L[u] = \frac{\partial u}{\partial x}+\frac{\partial^2 u }{\partial x \partial y} + \frac{\partial^3 u}{\partial y^3}$$中的 $$L = \frac{\partial}{\partial x}+\frac{\partial^2}{\partial x \partial y} + \frac{\partial^3}{\partial y^3}$$称为微分算子。
若两个微分算子$\mathcal{A}, \mathcal{B}$作用在充分光滑的任意函数$u$上时,会产生同样的结果,则称这两个微分算子$A, B$是等价的,记为$\mathcal{A} = \mathcal{B}$,此时有 $$\mathcal{A}[u] = \mathcal{B}[u]$$其中$u$是充分光滑的函数。
$\mathcal{A}, \mathcal{B}$为微分算子,$u$是充分光滑的函数。微分算子的和与积分别定义为
$$(\mathcal{A} + \mathcal{B}){[u]} = \mathcal{A}[u] + \mathcal{B}[u] \tag{1.1.4}$$
$$\mathcal{A}\mathcal{B}[u] = \mathcal{A}[\mathcal{B}[u]] \tag{1.1.5}$$
微分算子满足如下性质:
(1) 加法交换律
$$\mathcal{A} + \mathcal{B} = \mathcal{B} + \mathcal{A} \tag{1.1.6}$$
(2) 加法结合律
$$\mathcal{A} + (\mathcal{B} + \mathcal{C}) = (\mathcal{A} + \mathcal{B}) + \mathcal{C} \tag{1.1.7}$$
(3) 乘法结合律
$$\mathcal{A}(B\mathcal{C}) = (\mathcal{A}\mathcal{B})\mathcal{C} \tag{1.1.8}$$
(4) 乘法对加法的分配律
$$\mathcal{A}(\mathcal{B}+\mathcal{C}) = \mathcal{A}\mathcal{B} + \mathcal{A}\mathcal{C} \tag{1.1.9}$$
此外,对常系数微分算子成立:
(5) 乘法交换律
$$\mathcal{A}\mathcal{B} = \mathcal{B}\mathcal{A} \tag{1.1.10}$$
但乘法交换律可能对变系数微分算子不成立。
考虑$u,v$是充分光滑的函数,$c,d$为常数,若算子$\mathcal{L}$满足:
$$\mathcal{L}[cu + dv] = c\mathcal{L}[u] + d\mathcal{L}[v]. \tag{1.1.11}$$
则$\mathcal{L}$为线性算子。
1.1.3 叠加原理
对于线性偏微分方程的解,叠加原理成立;但对于非线性偏微分方程的解,叠加原理不成立。
叠加原理 Ⅰ 设$u_i$满足线性方程
$$\mathcal{L}u_i = f_i, i = 1, 2, \cdots, n$$
则它们的线性组合
$$u = \sum_{i = 1}^n{C_i u_i}$$
必满足方程
$$\mathcal{L}u = \sum_{i = 1}^n{C_i f_i}$$
特别的,当$u_i$均满足齐次方程时,$u$也满足该齐次方程。
叠加原理 Ⅱ 设$u_i$满足线性方程
$$\mathcal{L}u_i = f_i, i = 1, 2, \cdots$$
又假设它们的线性组合
$$u = \sum_{i = 1}^n{C_i u_i}$$
在求解域内一致收敛,且满足算子$\mathcal{L}$与该求和运算可交换的条件(即算子$\mathcal{L}$中出现的各阶偏导与该级数的求和运算都可交换运算次序),则$u$满足方程
$$\mathcal{L}u = \sum_{i = 1}^{\infty}{C_i f_i}$$
特别的,当$u_i$均满足齐次方程时,$u$也满足该齐次方程。
叠加原理 Ⅲ 设含连续参变量$M_0$的解族$u(M,M_0)$满足线性非齐次方程
$$\mathcal{L}u = f(M, M_0),$$
又假设积分
$$U(M) = \int{u(M, M_0)}dM$$
存在,且满足算子$\mathcal{L}$与该求和运算可交换的条件,则$U$满足方程
$$\mathcal{L}U = \int{f(M, M_0)}dM$$
特别的,当$u$满足齐次方程时,$U$也满足该齐次方程。
1.2 三类典型方程的建立
1.2 三类典型方程的建立
二阶线性偏微分方程可分为三大类,即双曲型方程、抛物型方程和椭圆型方程。它们的典型代表分别是
波动方程:
$$U_{tt} - a^2\sum^m_{j = 1}{\frac{\partial^2 U}{\partial x^2_j}} = f(x_1, x_2, \cdots, x_m, t).$$
热传导方程:
$$U_{t} - a^2\sum^m_{j = 1}{\frac{\partial^2 U}{\partial x^2_j}} = f(x_1, x_2, \cdots, x_m, t).$$
拉普拉斯方程:
$$\sum^m_{j = 1}{\frac{\partial^2 U}{\partial x^2_j}} = 0.$$
1.2.1 弦振动方程
一长为 $l$ 的柔软,均匀细弦拉紧以后,让它离开平衡位置在垂直于弦线的外力作用下作微小横震动 即弦的运动发生在同一平面内,且弦上各点的位移与平衡位置垂直,如图 1.1 所示,建立弦振动方程。
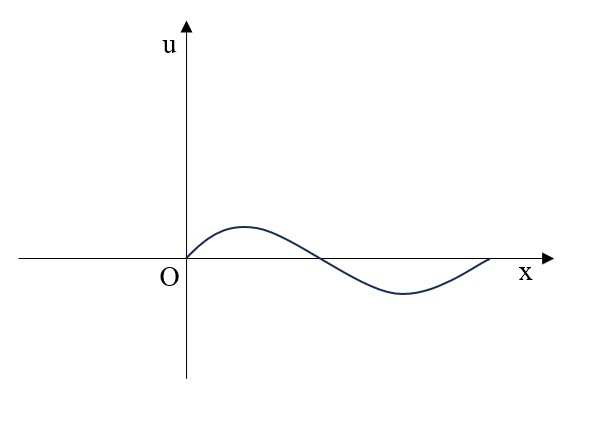
取弦的平衡位置为 $x$ 轴,在弦线运动的平面内,垂直于 $x$ 轴的直线为 $u$ 轴。这样,在任意 $t$ 时刻,弦线上点 $x$ 处的位移为
$$u = u(x, t)$$
简化假设:
1. 弦柔软,弦上任意一点的张力方向沿弦的切线方向。
2. 弦的横向振幅极小,张力与水平方向的夹角很小,弦的偏移与弦长相比很小,斜率的绝对值与 1 相比很小。
考虑弦上一段线元,即区间 $[x, x + \Delta x]$ 上的部分,其弦长为
$$ds = \int_{x}^{x + \Delta x} \sqrt{1 + \frac{\partial u}{\partial x}^2} dx \tag{1.2.1}$$
由于“弦的偏移与弦长相比很小,斜率的绝对值与 1 相比很小”,于是
$$(\frac{\partial u}{\partial x})^2 \ll 1,$$
即
$$1 + (\frac{\partial u}{\partial x})^2 \approx 1,$$
从而
$$ds \approx \int_{x}^{x + \Delta x} 1 dx = \Delta x.$$
这样,可认为区间 $[x, x + \Delta x]$ 上的这段弦在振动过程中并未伸长,因此由胡克定律可在,弦上每一点所受张力在运动过程中保持不变,即张力与时间无关。即点 $x$ 处的张力为 $T(x)$ ,张力方向始终沿着弦在点 $x$ 处的切线方向。
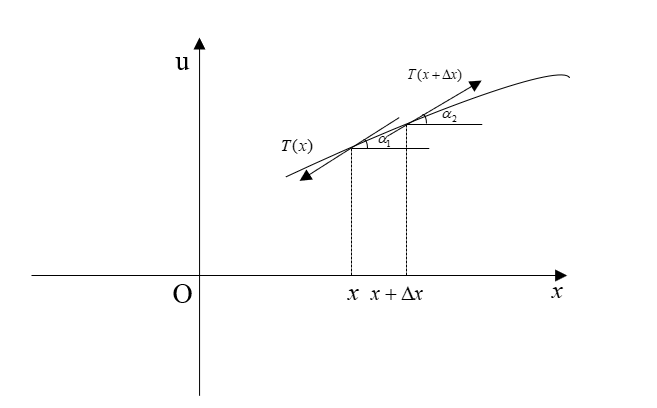
如图 1.2 所示,点 $x$ 处的张力 $T(x)$ 在 $x, u$ 两个方向上的分力分别为
$$-T(x)cos\alpha_{1}, -T(x)sin\alpha_{1},$$
其中 $\alpha_{1}$ 是点 $x$ 处的切线方向与 $x$ 轴正方向的夹角,负号表示力的方向取与坐标轴相反的方向。在弦的另一端 $x + \Delta x$ 处的张力 $T(x + \Delta x)$ 在 $x, u$ 两个方向上的分力分别为
$$T(x + \Delta x)cos\alpha_{2}, T(x + \Delta x)sin\alpha_{2}$$
其中 $\alpha_{2}$ 是点 $x$ 处的切线方向与 $x$ 轴正方向的夹角。
设弦的线密度为 $\rho$ ,弦段 $[x, x + \Delta x]$ 在质心 $\bar{a}$ 处的位移为 $u(\bar{x}, t)$ 则这一弦段质量与加速度的乘积为
$$\rho \Delta x \frac{\partial^2 u(\bar{x}, t)}{\partial x^2}$$
当弦不受外力作用时,据牛顿第二定律有
$$T(x + \Delta x)sin\alpha_{2} - T(x)sin\alpha_{1} = \rho \Delta x \frac{\partial^2 u(\bar{x}, t)}{\partial t^2} \tag{1.2.2}$$
$$T(x + \Delta x)cos\alpha_{2} - T(x)cos\alpha_{1} = 0 \tag{1.2.3}$$
由于 $(\frac{\partial u}{\partial x})^2 \ll 1$ ,所以
$$cos\alpha_{1} = \frac{1}{\sqrt{1 + tan\alpha_{1}^2}} = \frac{1}{\sqrt{1 + [\frac{\partial u(x, t)}{\partial x}]^2}} \approx 1 \tag{1.2.4}$$
$$cos\alpha_{2} = \frac{1}{\sqrt{1 + [\frac{\partial u(x + \Delta x, t)}{\partial x}]^2}} \approx 1 \tag{1.2.5}$$
$$sin\alpha_{1} \approx tan\alpha_{1} = \frac{\partial u(x, t)}{\partial x} \tag{1.2.6}$$
$$sin\alpha_{2} \approx tan\alpha_{2} = \frac{\partial u(x + \Delta x, t)}{\partial x} \tag{1.2.7}$$
于是,式 $(1.2.3)$ 变为
$$T(x + \Delta x) - T(x) = 0 \tag{1.2.8}$$
即
$$T(x + \Delta x) = T(x) = T$$
即张力 $T$ 是一个常数,从而式 $(1.2.2)$ 变为
$$T[\frac{\partial u(x + \Delta x, t)}{\partial x} - \frac{\partial u(x, t)}{\partial x}] - \rho \Delta x \frac{\partial^2 u(\bar{x}, t)}{\partial t^2} = 0 \tag{1.2.9}$$
应用微分中值定理得
$$T\frac{\partial^2 u(x + \theta \Delta x, t)}{\partial x^2}\Delta x - \rho \Delta x \frac{\partial^2 u(\bar{x}, t)}{\partial t^2} = 0, 0 < \theta < 1$$
约去 $\Delta x $ ,并令 $\Delta x \to 0$ ,此时 $x + \theta \Delta x \to x, \bar{x} \to x$;上式化为
$$T\frac{\partial^2 u(x, t)}{\partial x^2} - \rho \frac{\partial^2 u(x, t)}{\partial t^2} = 0$$
记 $\frac{T}{\rho} = a^2$ ,就得到不受外力作用时弦振动所满足的方程
$$\frac{\partial^2 u(x, t)}{\partial x^2} - a^2 \frac{\partial^2 u(x, t)}{\partial t^2} = 0 \tag{1.2.10}$$
当存在外力作用时,若在点 $x$ 处外力密度为$ F $ F = F(x,t) 即 t 时刻,
点 x 处的单位长度的弦所受平行于 u 轴方向的外力,则弦段 $[x, x + \Delta x]$ 上所受外力为
$$F(\tilde{x} , t)\Delta x, x \le \tilde{x} \le x + \Delta x$$
此时,式 $(1.2.9)$ 应修改为
$$T[\frac{\partial u(x + \Delta x, t)}{\partial x} - \frac{\partial u(x, t)}{\partial x}] - \rho \Delta x \frac{\partial^2 u(\bar{x}, t)}{\partial t^2} = -F(\tilde{x} , t)\Delta x \tag{1.2.11}$$
对上式左端应用微分中值定理,并 $\Delta x \to 0$ 得
$$T\frac{\partial^2 u(x + \theta \Delta x, t)}{\partial x^2}\Delta x - \rho \Delta x \frac{\partial^2 u(x, t)}{\partial t^2} = -F(x, t) \tag{1.2.12}$$
或
$$\frac{\partial^2 u(x, t)}{\partial x^2} - a^2 \frac{\partial^2 u(x, t)}{\partial t^2} = f(x, t) \tag{1.2.13}$$
其中, $f(x, t) = -\frac{F(x, t)}{\rho}$ 表示 $t$ 时刻单位质量的弦在点 $x$ 处所受的外力。
方程$(1.2.13)$描述了均匀弦的微小横震动的一般规律,人们称它为弦振动方程,也称一维波动方程。
附注 1.2.1 方程$(1.2.13)$还可以用来表述杆的纵振动(即一均匀细杆在外力作用下沿杆长方向作微小振动)。若取杆长方向作 $x$ 轴,取细杆的左端点$x = 0$,设$u(x, t)$为点$x$处的截面在$t$时刻沿着杆长方向的位移,那么由牛顿第二定律和胡克定律推得$u(x, t)$所适合的方程仍为方程$(1.2.13)$,其中$a^2 = \frac{Y}{\rho}$,$Y$为杨氏模量,$\rho$为杆的线密度。
杆的纵振动方程推导
考虑一长为 $l$ ,截面积为 $S$ ,体密度为 $\rho$ 的各向同性的均匀弹性细杆,沿杆的轴线方向做微小纵振动。
沿杆的轴线方向作 $x$ 轴,取细杆的左端点 $x = 0$ ,设 $u(x, t)$ 为点 $x$ 处质点在 $t$ 时刻的位移,则易知位于 $x$ 处的质点在 $t$ 时刻的相对伸长为 $u_{x}(x, t)$ 。
- 位移
由于振动,在不振动时位于 $x$ 的点,因振动偏离原平衡位置 $x$ ,位于 $x + u(x ,t)$ ,其中 $u(x, t)$ 为点 $x$ 处质点 $t$ 时刻的位移。 - 相对伸长
考虑细杆上一小段 $[x, x + dx]$ ,在不振动时这些一小段的两端分别位于平衡位置 $x$ 与 $x + dx$ 处;
因为振动,在 $t$ 时刻两端分别位于 $x + u(x, t)$ 与 $x + dx + u(x + dx, t)$ 处。
在 $t$ 时刻这一小段的长度为:
$$dl = [x + dx + u(x + dx, t)] - [x + u(x, t)] = dx + u(x + dx, t) - u(x, t)$$
不振动时这一小段的长度为:
$$dl_0 = x + dx - x = dx$$
振动导致的伸长为:
$$\Delta l = dl - dl_0 = u(x + dx, t) - u(x, t)$$
振动导致的相对伸长为:
$$\frac{\Delta l }{dl_0}= \frac{u(x + dx, t) - u(x, t)}{dx} = \frac{\partial u(x, t)}{\partial x} = u_{x}(x, t)$$ - 胡克定律
在弹性限度内,应力与应变成正比,比例系数称为杨氏模量 $Y$ ,即有 $\frac{F}{S} = Yu_{x}(x, t)$,其中 $F$ 为作用力,$S$ 为杆的截面积,$Y > 0$ 为杨氏模量。
取细杆上一小段 $[x, x + dx]$ 线元。这段线元的质量为
$$dm = \rho Sdx$$
在 $t$ 时刻其加速度为
$$a = u_{tt}(x, t)$$
在 $t$ 时刻,线元左右两端的相对伸长分别为
$$u_{x}(x, t), u_{x}(x + dx, t)$$
由胡克定律,在线元左端点必受到向左的拉力 $T_1$,大小为
$$T_1 = YSu_{x}(x, t)$$
在线元右端点必受到向右的拉力 $T_2$,大小为
$$T_2 = YSu_{x}(x + dx, t)$$
线元所受合力为
$$T = T_2 - T_1 = YSu_{x}(x + dx, t) - YSu_{x}(x, t)$$
由牛顿第二定律得
$$adm = T$$
即
$$\rho u_{tt}(x, t) = \frac{Y[u_{x}(x + dx, t) + u_{x}(x, t)]}{dx} = Yu_{xx}(x, t)$$
令 $a^2 = \frac{Y}{\rho}$
则得均匀细杆的纵振动方程为
$$u_{tt}(x, t) - a^{2}u_{xx}(x, t) = 0$$
若考虑弹性杆沿轴线方向上有一随时间变化的外力 $F$ ,其在 $t$ 时刻对点 $x$ 处在单位截面积上的作用力大小为 $F(x, t)$。
则$t$时刻线元所受的合力变为
$$T = T_2 - T_1 + f(t) = YSu_{x}(x + dx, t) - YSu_{x}(x, t) + SF(x, t)$$
则有
$$\rho u_{tt}(x, t) = \frac{Y[u_{x}(x + dx, t) + u_{x}(x, t)]}{dx} + \frac{F(x, t)}{dx} = Yu_{xx}(x, t) + F_{x}(x, t)$$
令 $a^2 = \frac{Y}{\rho}$
则得在轴线方向上受外力的均匀细杆的纵振动方程为
$$u_{tt}(x, t) - a^{2}u_{xx}(x, t) = \frac{1}{Y}F_{x}(x, t)$$
即
$$u_{tt}(x, t) - a^{2}u_{xx}(x, t) = f(x,t)$$
附注 1.2.2 若是考虑膜的振动或声音在空气中的传播,用来描述这些二维和三维波动现象的微分方程仍具有和方程$(1.2.13)$相似的形式
$$\frac{\partial^2 u}{\partial t^2}-a^2\Delta u = f(x_1, x_2, \cdots, x_m, t) \tag{1.2.14}$$
其中 $$\Delta = \sum^m_{j=1}{\frac{\partial^2}{\partial x^2_j}}$$
是$m$维拉普拉斯算子。通常称方程$(1.2.14)$为$m$维波动方程。
附注 1.2.3 对于弦和膜,它们都是柔软的,都具有只抗伸长、不抗弯曲的特性。也就是当它们发生形变时,反抗弯曲所产生的力矩可以忽略不计。在力学上被称作梁和板的抗伸长与完全的物体而言,其振动方程和平衡方程中将出现未知数的四阶微商。例如,梁的横震动方程
$$\frac{\partial^2 u}{\partial t^2}+a^2\frac{\partial^4 u}{\partial x^4} = 0 \tag{1.2.15}$$
参考文献
参考文献
[^1]: [1] 吴小庆.数学物理方程及其应用[M].科学出版社,2008.



