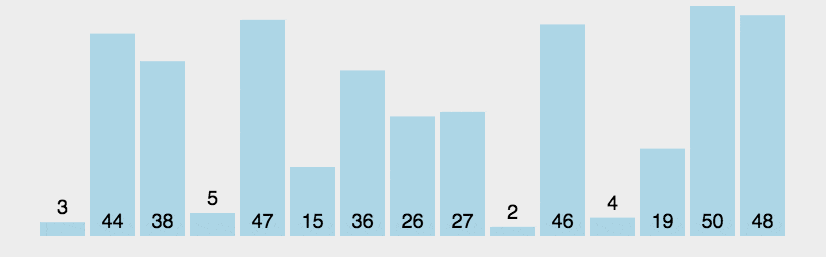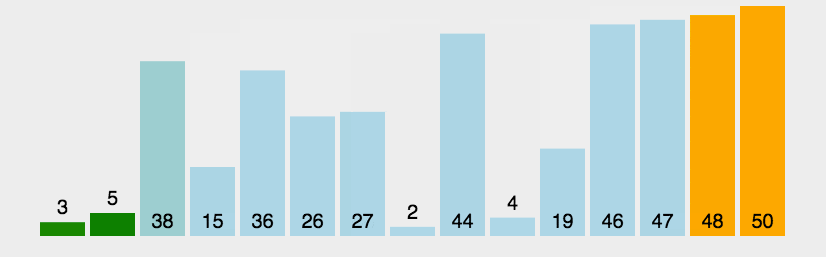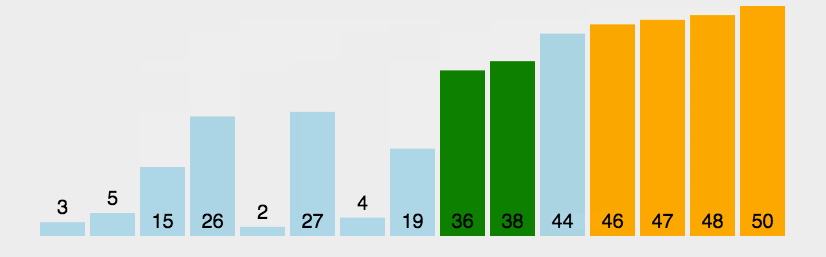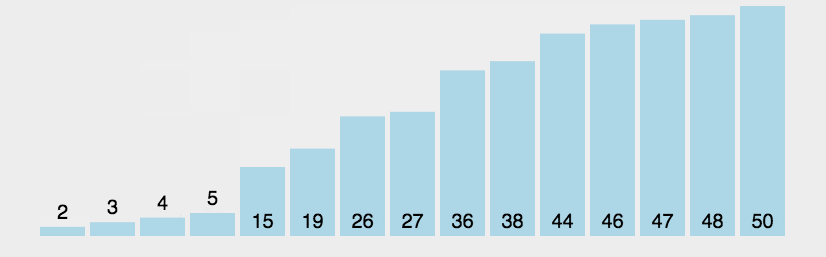封面图片 PID：1628397182442

HSMK の Mathematical Library 导航栏

排序算法

  排序算法是计算机程序设计中的一种基础算法，用于将一组数据按照一定的顺序进行排列。排序算法在许多领域都有广泛的应用，如数据库管理系统、数据挖掘、机器学习等。在完善我的项目hsmk-mathematical-library过程中，不可避免地要求实现一种或多种排序算法，就以本文作为项目实现的排序算法的详细文档。本文将介绍几种常见的排序算法，包括冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序、希尔排序、基数排序等。

前置内容

1. 算法复杂度

  算法复杂度是衡量算法性能的重要指标，包括时间复杂度和空间复杂度。时间复杂度表示算法执行所需的时间与输入规模之间的关系，空间复杂度表示算法执行所需的空间与输入规模之间的关系。

2. 算法稳定性

  算法稳定性是指在排序过程中，相同元素的相对位置是否发生变化。稳定的排序算法在排序过程中不会改变相同元素的相对位置，而不稳定的排序算法可能会改变相同元素的相对位置。

3. swap 函数

  因在下文中会给出不同语言的简单实现，在排序过程中，交换两个元素的位置是常见的操作，因此给出一个通用的交换函数，swap 函数。不同语言的实现不同，同一语言针对不同数据类型也有不同的实现方式，需要读者自行实现。在这里给出几个常见的实现方式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 1. 浅拷贝，交换指针指向的地址值
void swap(void **a, void **b){
    void *temp = *a;
    *a = *b;
    *b = temp;
}


// 2. 深拷贝，交换指针所指向的地址的内存块内容
void deepSwap(void *a, void *b, size_t size) {
  if (a == NULL || b == NULL || size == 0) return;
  if (a == b) return; // handle a == b
  void *temp = malloc(size);
  if (temp == NULL) return; // handle allocation failure
  memcpy(temp, a, size);
  memcpy(a, b, size);
  memcpy(b, temp, size);
  free(temp);
}

1
2
3
4
def swap(a, index1, index2):
  if a is None or index1 not in range(len(a)) or index2 not in range(len(a)): return
  if index1 == index2: return
  a[index1], a[index2] = a[index2], a[index1]
1
2
3
4
5
6
7
public static void swap(Object[] a, int index1, int index2) {
  if (a == null || index1 < 0 || index2 < 0 || index1 >= a.length || index2 >= a.length) return;
  if (index1 == index2) return;
  Object temp = a[index1];
  a[index1] = a[index2];
  a[index2] = temp;
}

4. compare/compareTo 函数

  在排序过程中，需要比较两个元素的大小，因此给出一个通用的比较函数，compare 函数与 compareTo 函数（作为对象的成员方法）。不同语言的实现不同，同一语言针对不同数据类型也有不同的实现方式，需要读者自行实现。在本文，规定函数的返回值如下：

函数调用 返回值 说明
compare(a, b) -1 a < b
compare(a, b) 0 a == b
compare(a, b) 1 a > b
a.compareTo(b) -1 a < b
a.compareTo(b) 0 a == b
a.compareTo(b) 1 a > b 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 1. 比较两个整数的大小
int compare(int a, int b){
  if (a < b) return -1;
  if (a == b) return 0;
  if (a > b) return 1;
}

// 2. 比较两个浮点数的大小
int compare(double a, double b){
  if (a < b) return -1;
  if (a == b) return 0;
  if (a > b) return 1;
}

1
2
3
4
def compare(a, b):
  if a < b: return -1
  if a == b: return 0
  if a > b: return 1

下文所有排序的默认次序均为升序即从小到大。

1. 冒泡排序

定义

经典的冒泡排序[1] 冒泡排序参考资料是一种较易理解和实现的排序算法，由于在算法的执行过程中，较小的元素像是气泡般慢慢「浮」到数列的顶端，故叫做冒泡排序。

过程

它的工作原理是每次检查相邻两个元素，如果前面的元素与后面的元素满足给定的排序条件，就将相邻两个元素交换。当没有相邻的元素需要交换时，排序就完成了。对于 $n$ 个元素的数列，经过 $i$ 次扫描后，数列的末尾 $i$ 项必然是最大的$i$项，因此冒泡排序最多需要扫描 $n-1$ 遍数组就能完成排序。
一个简单的示意图如下:
冒泡排序

性质

在序列完全有序时，冒泡排序只需遍历一遍数组，不用执行任何交换操作，时间复杂度为 $O(n)$ 。

在最坏情况下，冒泡排序要执行 $\frac{n(n-1)}{2}$ 次交换操作，时间复杂度为 $O(n^2)$ 。

冒泡排序的平均时间复杂度为 $O(n^2)$ 。

算法 时间复杂度 空间复杂度 稳定性
冒泡排序 $O(n^2)$ $O(1)$ 稳定

代码实现

伪代码 采用类C格式，数组下标从0开始

latex code 
1
2
3
4
5
6
7
8
9
\begin{array}{l}\\
1\quad\textbf{Input. } \text{An array } A \text{ consisting of }n\text{ elements.}\\
2\quad\textbf{Output. } A\text{ will be sorted in nondecreasing order stably.}\\
3\quad\textbf{Method. }\\
4\quad\textbf{for }i\gets0\textbf{ to }n-1\\
5\quad\qquad\textbf{for }j\gets0\textbf{ to }n-1-i\\
6\quad\qquad\qquad\textbf{if }A[j]>A[j+1]\\
7\quad\qquad\qquad\qquad \text{Swap } A[j]\text{ and }A[j+1]
\end{array}

sort_fakecode_1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @brief 冒泡排序算法的简单实现
 * @param arr 将要被排序的数组
 * @param arrLen 数组的长度
 */
void bubbleSort(int *arr, int arrLen){
  /**
   * 遍历数组，并比较相邻元素
   * 如果元素顺序不正确，交换它们
   */
  for(int i = 0; i < arrLen; i++){
    for (int j = 0; j < arrLen - i - 1 ; j++){
      if (arr[j] > arr[j + 1]) {
        int temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        // or swap(&arr[j], &arr[j + 1], sizeof(int));
      }
    }
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
void bubbleSort(int[] arr){
  for(int i = 0; i < arr.length; i++){
    for (int j = 0; j < arr.length - i - 1 ; j++){
      if (arr[j] > arr[j + 1]) {
        int temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        // or swap(arr, j, j + 1);
      }
    }
  }
}
1
2
3
4
5
6
def bubbleSort(arr):
  for i in range(len(arr)):
    for j in range(len(arr) - i - 1):
      if arr[j] > arr[j + 1]:
        arr[j], arr[j + 1] = arr[j + 1], arr[j]
        # or swap(arr, j, j + 1)

有许多人对冒泡排序做了相当的改进/优化，简要介绍几种常见的优化方法[2] 胡伟东.冒泡排序算法的几种优化与变形[J].电脑编程技巧与维护参考资料。

在排序过程中可能出现排序未完成但待排序数组已经有序的情况，在这种情况下再使用冒泡排序并不会出现元素交换的情况。所以可以设置一个标志变量，在一次排序过程中，若发生了交换，就改变标志变量的值，否则就不变。完成一次排序后，如果标志变量的值不变，说明数组已经有序，可以退出排序。

伪代码如下:

latex code 
1
2
3
4
5
6
7
8
9
10
11
12
13
\begin{array}{l}\\
1\quad\textbf{Input. } \text{An array } A \text{ consisting of }n\text{ elements.} \\
2\quad\textbf{Output. } A\text{ will be sorted in nondecreasing order stably.} \\
3\quad\textbf{Method. }  \\
4\quad\textbf{for }i\gets0\textbf{ to }n-1\\
5\quad\qquad flag = false\\
6\quad\qquad\textbf{for }j\gets0\textbf{ to }n-1-i\\
7\quad\qquad\qquad\textbf{if }A[j]>A[j+1]\\
8\quad\qquad\qquad\qquad\text{Swap } A[j]\text{ and }A[j+1]\\
9\quad\qquad\qquad\qquad flag = true\\
10\quad\qquad\textbf{if }flag = true\\
11\quad\qquad\qquad\textbf{break}
\end{array}

sort_fakecode_2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * @brief 冒泡排序算法的简单实现
 * @param arr 将要被排序的数组
 * @param arrLen 数组的长度
 */
void bubbleSort(int *arr, int arrLen){
  /**
   * 遍历数组，并比较相邻元素
   * 如果元素顺序不正确，交换它们
   */
  for(int i = 0; i < arrLen; i++){
    int flag = 0;
    for (int j = 0; j < arrLen - i - 1 ; j++){
      if (arr[j] > arr[j + 1]) {
        int temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        // or swap(&arr[j], &arr[j + 1], sizeof(int));
        flag = 1;
      }
    }
    if (flag == 0) break;
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void bubbleSort(int[] arr){
  for(int i = 0; i < arr.length; i++){
    boolean flag = false;
    for (int j = 0; j < arr.length - i - 1 ; j++){
      if (arr[j] > arr[j + 1]) {
        int temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        // or swap(arr, j, j + 1);
        flag = true;
      }
    }
    if(!flag) break;
  }
}
1
2
3
4
5
6
7
8
9
def bubbleSort(arr):
  for i in range(len(arr)):
    flag = False
    for j in range(len(arr) - i - 1):
      if arr[j] > arr[j + 1]:
        arr[j], arr[j + 1] = arr[j + 1], arr[j]
        # or swap(arr, j, j + 1)
        flag = True
    if not flag: break

考虑序列[2, 3, 4, 5, 9, 8, 7]，采用“上冒”，第一轮排序结束后为[2, 3, 4, 5, 8, 7, 9]。可以发现，当 7 和 9 交换位置后，后续的数字都没有互换，即在后续的排序中[2, 3, 4, 5]不需要参与排序。得出结论：每轮遍历的区间边界都是由上一轮遍历最后一次发生交换的位置决定的。这样一来，可以引入标记变量 last 记录每轮排序最后一次交换的位置，并将 last 赋给下一轮遍历区间的终点。大大缩小了下一轮排序遍历区间，快速收缩待排序范围，从而提高了算法效率。

伪代码如下:

latex code 
1
2
3
4
5
6
7
8
9
10
11
12
13
\begin{array}{l}\\
1\quad\textbf{Input. } \text{An array } A \text{ consisting of }n\text{ elements.} \\
2\quad\textbf{Output. } A\text{ will be sorted in nondecreasing order stably.} \\
3\quad\textbf{Method. }  \\
4\quad\textbf{for }i\gets0\textbf{ to }n-1\\
5\quad\qquad last = 0\\
6\quad\qquad\textbf{for }j\gets last\textbf{ to }n-1-i\\
7\quad\qquad\qquad\textbf{if }A[j]>A[j+1]\\
8\quad\qquad\qquad\qquad\text{Swap } A[j]\text{ and }A[j+1]\\
9\quad\qquad\qquad\qquad last = j\\
10\quad\qquad\textbf{if }last = 0\\
11\quad\qquad\qquad\textbf{break}
\end{array}

sort_fakecode_3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * @brief 冒泡排序算法的简单实现
 * @param arr 将要被排序的数组
 * @param arrLen 数组的长度
 */
void bubbleSort(int *arr, int arrLen){
  /**
   * 遍历数组，并比较相邻元素
   * 如果元素顺序不正确，交换它们
   */
  for(int i = 0; i < arrLen; i++){
    int last = 0;
    for (int j = last; j < arrLen - i - 1 ; j++){
      if (arr[j] > arr[j + 1]) {
        int temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        // or swap(&arr[j], &arr[j + 1], sizeof(int));
        last = j;
      }
    }
    if (last == 0) break;
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void bubbleSort(int[] arr){
  for(int i = 0; i < arr.length; i++){
    int last = 0;
    for (int j = last; j < arr.length - i - 1 ; j++){
      if (arr[j] > arr[j + 1]) {
        int temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        // or swap(arr, j, j + 1);
        last = j;
      }
    }
    if(!last) break;
  }
}
1
2
3
4
5
6
7
8
9
def bubbleSort(arr):
  for i in range(len(arr)):
    last = 0
    for j in range(last, len(arr) - i - 1):
      if arr[j] > arr[j + 1]:
        arr[j], arr[j + 1] = arr[j + 1], arr[j]
        # or swap(arr, j, j + 1)
        last = j
    if not last: break

经典的冒泡算法中可以发现，经典的冒泡排序是从一端开始比较的，经过第 1 轮排序后，一端为极值点，如此重复处理完成排序。若在实现一端有序的同时，从另一端也进行排序，使另一端也为极值点，即实现双向冒泡排序。

  1. 第 1 轮从左向右，将最大值移到右端点
  2. 第 2 轮从右向左，将最小值移到左端点
  3. 重复 1、2 步，直到数组有序

伪代码如下:

latex code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
\begin{array}{l}\\
1\quad\textbf{Input. } \text{An array } A \text{ consisting of }n\text{ elements.} \\
2\quad\textbf{Output. } A\text{ will be sorted in nondecreasing order stably.} \\
3\quad\textbf{Method. }  \\
4\quad left=0;right=n-1\\
5\quad\textbf{while }left<right\\
6\quad\qquad\textbf{for }i\gets left\textbf{ to }right\\
7\quad\qquad\qquad\textbf{if }A[i]>A[i+1]\\
8\quad\qquad\qquad\qquad\textbf{Swap}(A[i],A[i+1])\\
9\quad\qquad\qquad\qquad right = i\\
10\quad\qquad\textbf{for }i\gets right\textbf{ to }left\\
11\quad\qquad\qquad\textbf{if }A[i]<A[i-1]\\
12\quad\qquad\qquad\qquad\textbf{Swap}(A[i],A[i-1])\\
13\quad\qquad\qquad\qquad left = i\\
\end{array}

sort_fakecode_4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * @brief 冒泡排序算法的简单实现
 * @param arr 将要被排序的数组
 * @param arrLen 数组的长度
 */
void bubbleSort(int *arr, int arrLen){
  /**
   * 遍历数组，并比较相邻元素
   * 如果元素顺序不正确，交换它们
   */
  int left = 0, right = arrLen - 1;
  while(left < right){
    for(int i = left; i < right; i++){
      if (arr[i] > arr[i + 1]) {
        int temp = arr[i];
        arr[i] = arr[i + 1];
        arr[i + 1] = temp;
        // or swap(&arr[i], &arr[i + 1], sizeof(int));
        right = i;
      }
    }
    for(int i = right; i > left; i--){
      if (arr[i] < arr[i - 1]) {
        int temp = arr[i];
        arr[i] = arr[i - 1];
        arr[i - 1] = temp;
        // or swap(&arr[i], &arr[i - 1], sizeof(int));
        left = i;
      }
    }
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void bubbleSort(int[] arr){
  int left = 0, right = arr.length - 1;
  while(left < right){
    for(int i = left; i < right; i++){
      if (arr[i] > arr[i + 1]) {
        int temp = arr[i];
        arr[i] = arr[i + 1];
        arr[i + 1] = temp;
        // or swap(arr, i, i + 1);
        right = i;
      }
    }
    for(int i = right; i > left; i--){
      if (arr[i] < arr[i - 1]) {
        int temp = arr[i];
        arr[i] = arr[i - 1];
        arr[i - 1] = temp;
        // or swap(arr, i, i - 1);
        left = i;
      }
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def bubbleSort(arr):
  left = 0
  right = len(arr) - 1
  while(left < right):
    for i in range(left, right):
      if arr[i] > arr[i + 1]:
        arr[i], arr[i + 1] = arr[i + 1], arr[i]
        # or swap(arr, i, i + 1)
        right = i
    for i in range(right, left, -1):
      if arr[i] < arr[i - 1]:
        arr[i], arr[i - 1] = arr[i - 1], arr[i]
        # or swap(arr, i, i - 1)
        left = i

参考文献

[1]
 冒泡排序
[2]
 胡伟东.冒泡排序算法的几种优化与变形[J].电脑编程技巧与维护